High school physics courses usually begin with a study of classical mechanics. Early in the course students are introduced to the equations of motion, the kinematics equations.
Kinematics
Kinematics is the study of the motion of objects without concern for the forces causing the motion. These familiar equations allow students to analyze and predict the motion of objects, and students will continue to use these equations throughout their study of physics. A solid understanding of these equations and how to employ them to solve problems is essential for success in physics. This article is a purely mathematical exercise designed to provide a quick review of how the kinematics equations are derived using algebra.
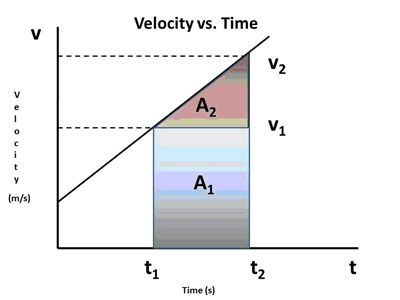
This exercise references the diagram in Fig. 1, in whichthe x axis represents time and the y axis represents velocity. The diagonal line represents the motion of an object, with velocity changing at a constant rate. The shaded area (A1 + A2) represents the displacement of the object during the time interval between t1 and t2, during which the object increased velocity from v1 to v2.
This document will make use of the following variables:
v = the magnitude of the velocity of the object (meters per second, m/s)
v1 = the magnitude of the initial velocity (meters per second, m/s) (in some texts this is vi or v0)
v2 = the magnitude of the final velocity (meters per second, m/s) (in some texts this is vf)
a = the magnitude of the acceleration (in meters per second squared, m/s2)
s = the displacement vector, the magnitude of the displacement is the distance,
s = │s│ = d (vectors are indicated in bold; the same symbol not in bold represents the magnitude of the vector)
Δ indicates change, for example Δv = (v2 —v1)
t = time
t1 = the initial time
t2 = the final time
How to derive the equations
The first step will be to calculate the slope of the diagonal line. In this case, since the slope will be a change in velocity (rise) divided by a change in time (run), the slope will equal the acceleration.
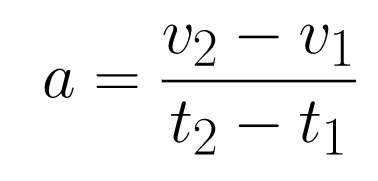
To keep things simple, rewrite t2 — t1 as Δt.
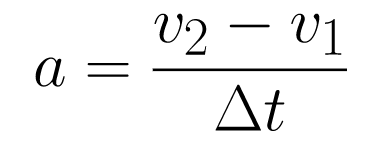
This is Equation 1. Rearrange Equation 1 to get v2 on the left side of the equation. This expresses the equation in the slope-intercept form of a line, y = mx + b.
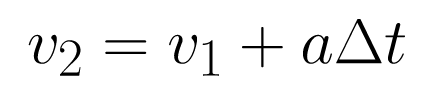
To get the next equation, derive an expression for the displacement of the object during the time interval, Δt. The displacement for an object traveling at a constant velocity can be found by multiplying the object’s velocity by the time the object travels at that velocity.
The object in this activity, however, is not traveling at a constant velocity. How can the distance be calculated for an object that is not traveling at a constant velocity?
Consider an object moving with constant velocity, v1, from time t1 to t2. The displacement of the object is represented by s. The absolute value of the displacement is the distance traveled. The displacement can be calculated by:
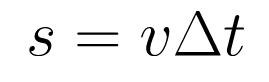
Where Δt is the time interval t2 — t1. Consider a graph of the motion of this object, as in Fig. 2.figure 2
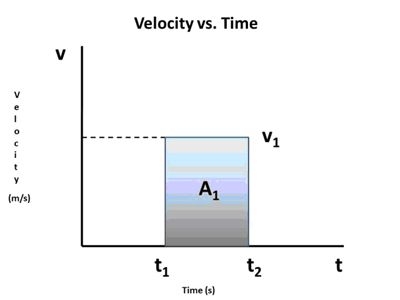
The displacement of the object in Fig. 2 is equal to v1Δt. The product, v1Δt, is also equal to the area A1. Similarly, the total displacement of the object in Fig. 1, which is moving at a changing velocity, can be found by calculating the area under the line during the time interval, Δt. For some objects this calculation can be a little tricky, but for the object depicted in Fig. 1, calculating the area under the line simply means calculating the area of the rectangle A1 and the triangle A2 and adding the values.
Area A1 is a rectangle. The length, l, is v1. The width, w, is t2 — t1, (Δt).
Area of rectangle A1 = l x w
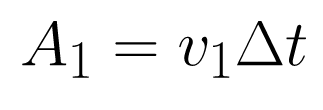
Area A2 is a triangle with base Δt and height v2 — v1.
Area of triangle A2 = ½ b x h
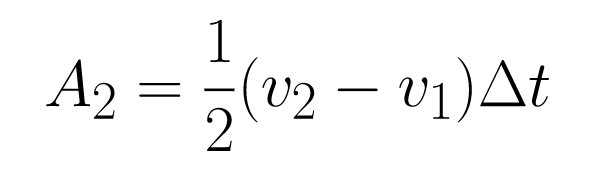
Adding areas A2 and A1 gives the total displacement of the object during the time interval.
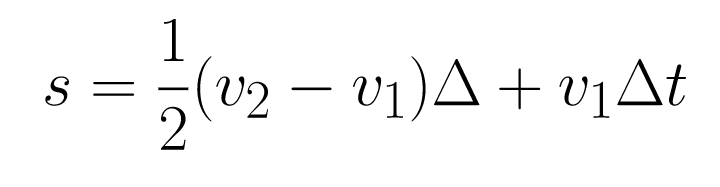
Substituting for A2 and A1 gives:
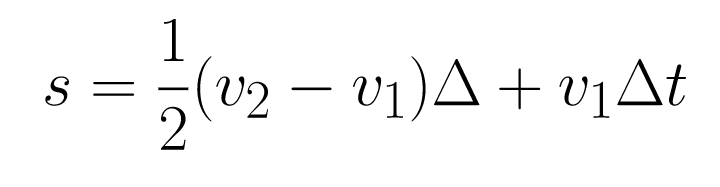
Simplifying:
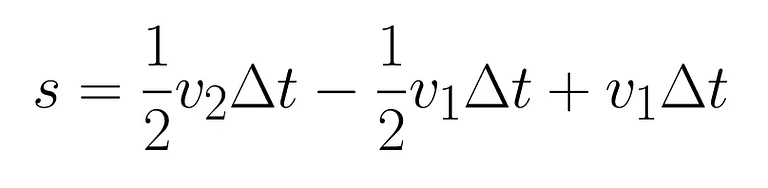
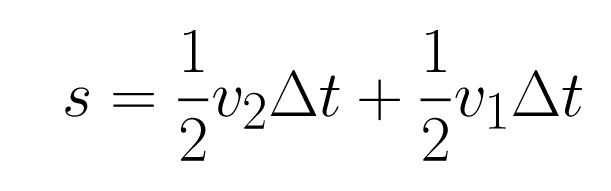
This is Equation 2.
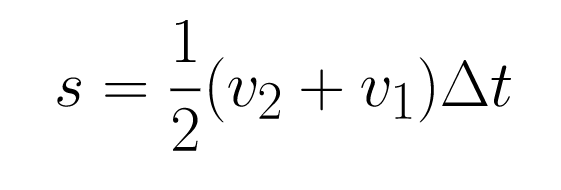
Equation 1 does not include the variable s. Equation 2 does not include the variable a. The remaining kinematics equations can be found by eliminating the variables v2 and Δt. Initial velocity, v1, is still in every equation, but v1 can often be set to zero if the object starts from rest.
Writing a set of equations, each with one or more variables eliminated, will provide a set of equations that can be used in a wide variety of problems, depending on what information is given.
Equation 3 is found by eliminating v2.
Start with Equation 1.
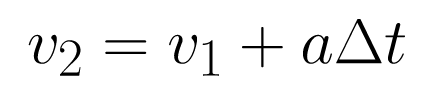
By applying some algebra, the left side of this equation can be made to look like the right side of Equation 2.Whatever is done to one side of the equation must be done to the other side of the equation.
Add v1 to both sides.
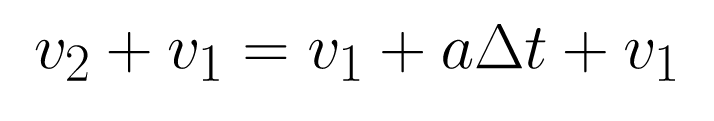
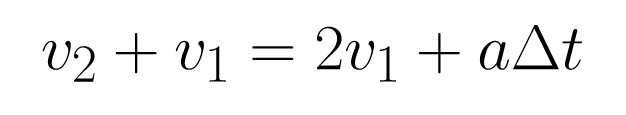
Now multiply both sides by (1/2)Δt.
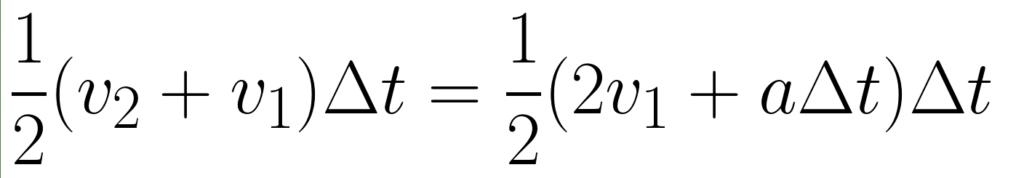
Substituting the left side of the equation for s eliminates v2 and gives:
Equation 3.
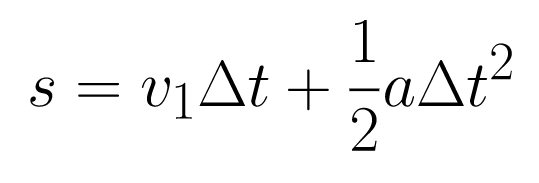
Equation 4 is found by eliminating the variable of time, or Δt.
Begin with Equation 1 rearranged with acceleration on the left side of the equals sign:
Equation 1.
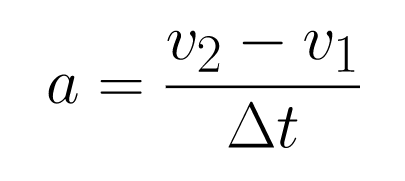
Multiply the left side of Equation 2 by the left side of Equation 1, and multiply the right side of Equation 2 by the right side of Equation 1.
Doing this means multiplying both sides by acceleration, but this will allow Δt to cancel on the right side of the equation.
Equation 2.
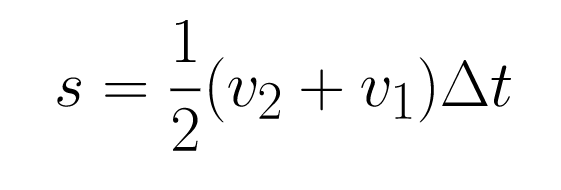
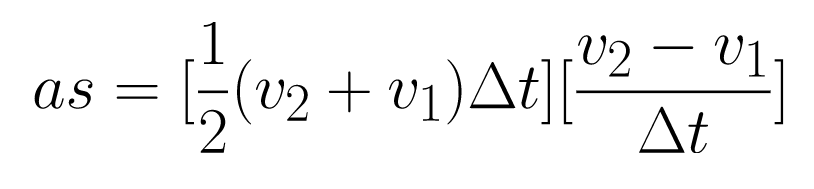
Δt cancels out, and the equation simplifies to:
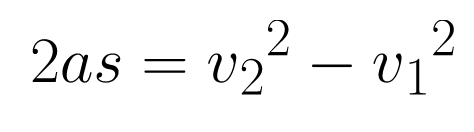
This equation is often written as:
Equation 4.
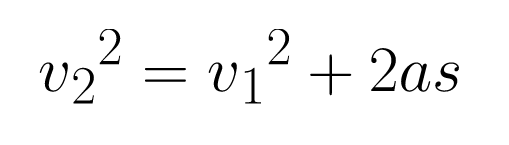
Here are all four of the standard kinematics equations:
Equation 1.
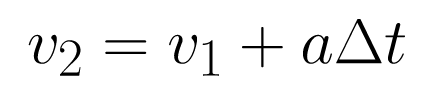
Equation 2.
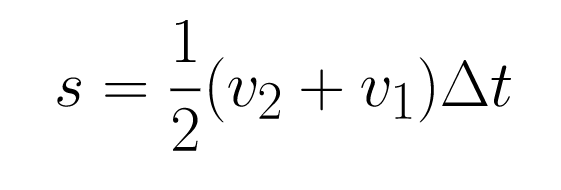
Equation 3.
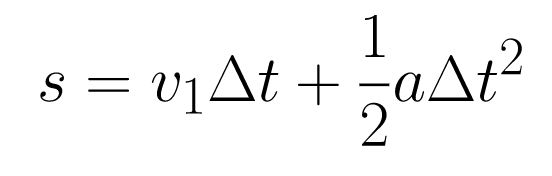
Equation 4.
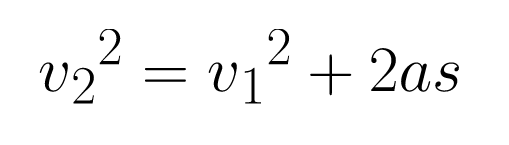
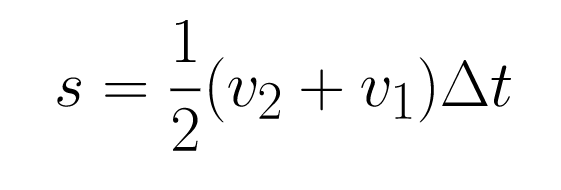
Resources
Students can apply the kinematics equations when conducting investigations with these products: