An Experiment in Circular Motion and Centripetal Acceleration
The conical pendulum lab allows students to investigate the physics and mathematics of uniform circular motion. A motorized, plastic plane* is suspended from a thin string and “flies” in a circular path with a constant speed. The plane and the supporting string trace a conical pendulum. Students measure the velocity of the plane directly and then compare that value to the velocity predicted by analyzing the forces acting on the plane. This lab is appropriate for AP® Physics and physics students with strong algebra and geometry backgrounds.
Materials
- Flying Plane
- 2 AA Batteries
- Meter Stick or Tape Measure
- Timer or Stopwatch
- Laser Pointer
- Scientific Calculator
*Other motorized objects are often used for the pendulum bob in this experiment, including the popular “flying pig.” The procedures and the calculations are the same, as long as the pendulum and the string trace out a conical pendulum, and the pendulum moves with uniform circular motion.
Safety
Make sure the plane is mounted securely and will not break loose during flight. First, check that the battery compartment of the plane is securely fastened. Ensure that no one is in the path of the plane. Wear safety glasses to prevent eye injury. Use caution when using the laser and do not look directly into the laser beam.
Procedure
Part I: Launch the Plane
Install the batteries in the plane’s battery compartment. Turn on the switch to test that the batteries are installed correctly and that the plane is functioning properly. Next, you will need to suspend your plane from the ceiling or other suitable structure that allows the plane and the support string a clear flight path.
Once the plane is suspended, move the switch to the on position. The propeller will begin to turn. Hold the plane to the side of its resting position and give the plane a gentle push in a direction tangent to a circular course. This may take a few attempts, but once done correctly the plane will settle into a regular circular pattern, and you will be able to see the plane and the string trace out a conical pendulum.
Part II: Measure the Tangential Velocity
Calculate the average speed of the plane by dividing the distance it travels in 1 revolution (the circumference) by the time for 1 revolution (or the period).
Step 1: Measure the circumference by finding the radius of the plane’s flight and calculating the circumference with the equation C = 2Ï€r, where C is the circumference, r is the radius, and Ï€ is 3.14. While the plane is in flight, hold a laser vertically and shine the light on the ceiling or floor (depending on how the plane is mounted), so that the plane crosses the beam. Mark this position on the ceiling or floor, and measure to the center of the plane’s path. This is the radius of the plane’s circular flight path.
Record the radius here: ___________________ (meters)
Step 2: Find the period, or the time for a single revolution. To do this, use a timer or stopwatch to measure the time it takes for the plane to make 10 complete revolutions, and divide by 10.
Record the time for 10 revolutions here: _______________ (seconds)
Record the time for 1 revolution here: _______________ (seconds)
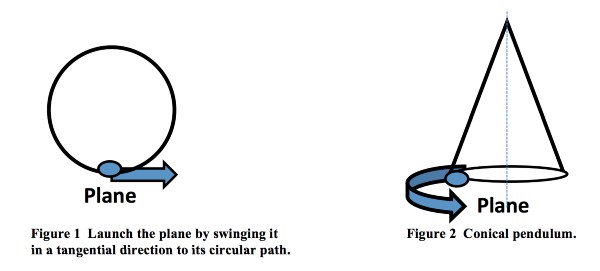
Step 3: Finally, divide the circumference by the period. The speed is found by dividing the distance traveled by the time. Write an equation for the plane’s speed (v) in the space provided below.
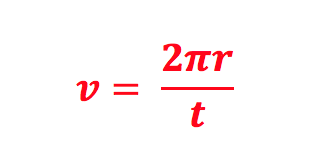
This value is the magnitude of the plane’s tangential velocity, or its speed. Record the magnitude of the tangential velocity here: _______________ (meters per second)
Answer the following questions from Part II:
Q: This lab involves “uniform circular motion.” What is uniform circular motion, and does the plane’s motion fit this definition?
A: Uniform circular motion describes an object moving in a circular path at a constant speed. The plane is moving in uniform circular motion.
Q: Are the plane’s velocity and speed the same? Are the plane’s velocity and speed both constant?
A: No. Speed and velocity are not the same. The plane’s speed is a scalar quantity and is constant. The speed is the magnitude of the plane’s velocity. Velocity is a vector. The plane’s velocity is constantly changing, because it is constantly changing direction.
Q: What is applying the force to the plane that causes it to constantly change direction? Where is this force pointing? What term do we use for this type of force? Is there an equation for this type of force?
A: The tension in the string pulls the plane up and in. The horizontal component of the tension pulls the plane toward the center of the circle, causing the plane to move in a circular path. This is called a centripetal force. The equation for centripetal force is Fc = mv 2/r, where m is the mass of the object, v is the tangential velocity, and r is the radius of the circular path.
Part III: Calculate the Theoretical Speed of the Plane Using Forces and the Laws of Motion
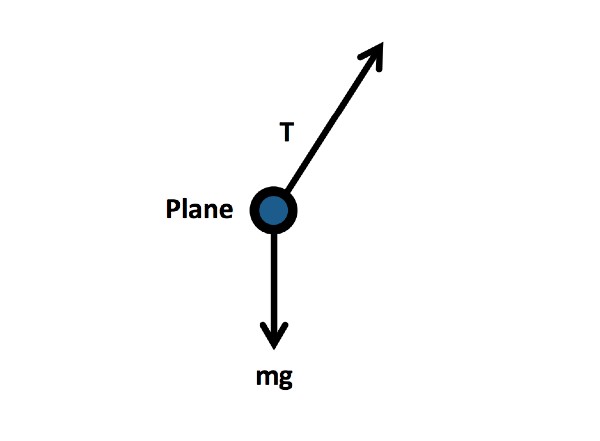
Step 1: In the space below, draw a free body diagram of the forces acting on the plane while it is in flight.
T = tension
m = mass
g = acceleration due to gravity (9.8 m/s2 )
(The force from the propeller is directed in or out of the page, depending on which way the plane is flying.)
Step 2: Resolve the components of the forces from the diagram in Step 1 to horizontal and vertical components, and find a mathematical expression for these components in terms of the forces in Step 1.
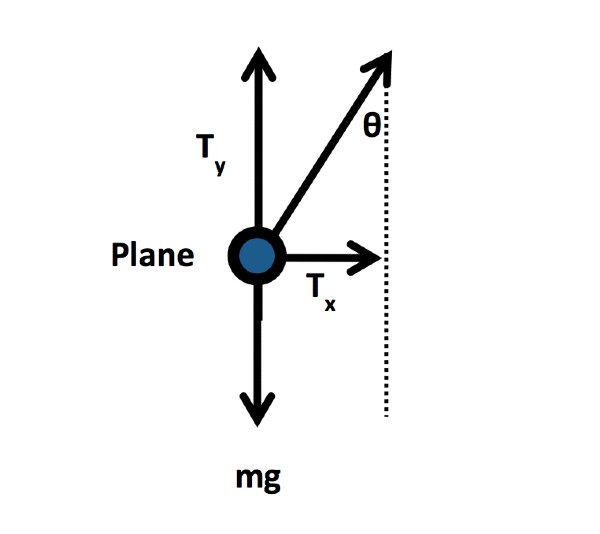
Tx = horizontal component of tension
Ty = vertical component of tension
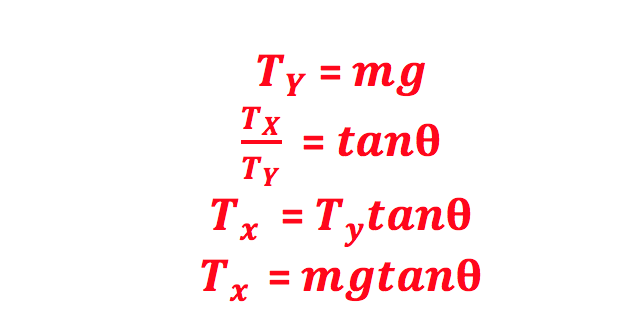
Step 3: Set the horizontal component of the tension equal to the centripetal force causing the plane to move in a circle.
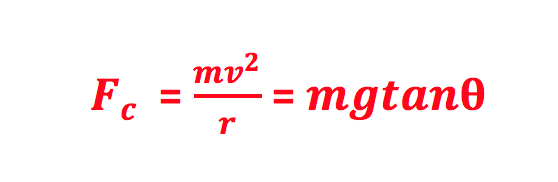
Step 4: Solve this equation for velocity.
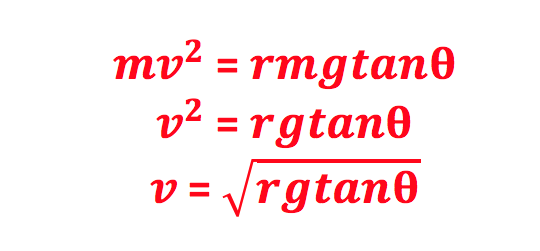
Here, v is the magnitude of the tangential velocity of the plane, or the speed.
Step 5: Find θ by measuring the length of the string (from the pivot point to the center of the plane) and the radius (follow the procedure in Part II, Step 1).
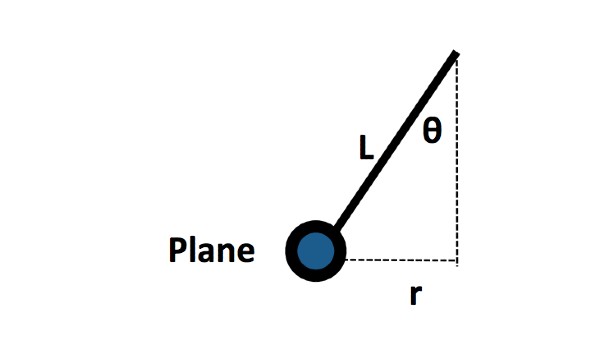
L = length of the string (meters)
r = radius of the circular path (meters)
θ = angle between the string and the vertical (degrees)
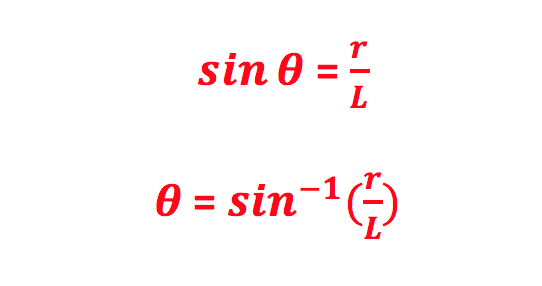
Record your measurements here:
r = ______________ (meters)
L = __________________ (meters)
sinθ = _______________
θ = __________________ (degrees)
Step 6: Substitute the value for θ from Step 5 into the equation for velocity from Step 4 and solve for the velocity of the plane.
Step 7: Compare the value given by the calculation in Step 6 with the value measured in Part II. Calculate the percent difference in the 2 values. Are the values the same? What are the sources of error in the calculations?
Sources in error include human error while measuring the length of the string, the radius of the circle, and the measurement of the period of revolution. The plane is a fairly large pendulum bob. Finding the exact point from which to measure the radius using a laser pointer is a likely source of error.

Answer the following questions from Part III:
Q: Based on the free body diagram you drew, explain the motion of the plane. Why does the plane move in a horizontal circle, and why doesn’t the plane move up and down?
A: The forces on the plane in the vertical direction are balanced so the plane does not move up and down. The horizontal component of the tension is not balanced and always points toward the center of the circle, while the thurst from the plane’s propeller is always directed tangent to the plane’s circular path.
Q: Is it necessary to measure the mass of the plane?
(Hint: See Part III, Step 3.)
A: The mass of the plane cancels out when you set the equation for centripetal force equal to the horizontal component of the tension. It is not necessary to measure the mass of the plane.
Emmette Cox
Product Developer
AP® is a trademark registered and/or owned by the College Board®, which was not involved in the production of, and does not endorse, this product.





1 Comment
Interesting experiment with the conical pendulum! I never would have thought that the shape of the pendulum would affect its swinging motion so drastically. Great job explaining the physics behind it as well. I’ll have to try this experiment with my kids and see their reactions!