The ring and disc investigation is a classic physics demonstration designed to introduce the concepts of rotational inertia, rotational motion, and rolling motion. Both the disc and the ring have the same diameter, width, and mass. When simultaneously released from rest at the same point on an inclined plane, the disc accelerates faster, reaching the end of the incline first. The ring and disc demonstration can also be used to teach techniques for solving problems in rotational motion.
Objective:
In this activity students use their knowledge of rotational motion and kinematics to predict how long it will take each object to reach the bottom of an inclined plane.
Standards:
NGSS
SEPs
- Planning and Carrying Out Investigations
- Analyzing and Interpreting Data
- Using Mathematics and Computational Thinking
DCIs
PS2: Forces and Motion
- PS2.A: Forces and Motion
- PS2.C: Stability and Instability in Physical System
CCCs
PS2: Forces and Motion
- Scale, Proportion, and Quantity
- Systems and System Models
Unit 1: Kinematics
Unit 2: Force and Translational Dynamics
Practice:
- 1. Creating Representations
- Mathematical Routines
Unit 1: Kinematics
Unit 2: Force and Translational Dynamics
Unit 5: Torque and Rotational Dynamics
Practice:
- Creating Representations
- Mathematical Routines
Students should gain a better understanding of the moment of inertia and how the distribution of mass in a rigid object determines how applied forces affect the object’s motion. Students test their calculations by analyzing the motion of the objects with timers or probeware sensors.
This activity is appropriate for students in honors or AP® Physics courses who have a strong background in algebra, geometry, and trigonometry.
Needed Materials
- Ring and Disc Set
- Meter Stick or Metric Tape Measure
- Metric Ruler
- Timer
- Calculator with Trigonometric Functions
- Inclined Plane
- Support for Plane
- Go Direct® Acceleration Sensor (optional)
- Computer or tablet (optional)
- Digital camera (optional)
Safety
Procedure
Part I: Demonstration
This demonstration is a good way to introduce rotational inertia and begin a discussion of rotational and rolling motion. Set up an inclined plane with an angle of about 5 to 10° and use a meter stick to keep the ring and disc at the same place on the top of the incline. Before moving the stick, students can predict if one object will move faster and if so, which one. Quickly move the meter stick and allow the objects to roll to the bottom. The disc will reach the bottom of the inclined plane first. After the demonstration, discuss why the disc reached the bottom first. As an extension, incorporate motion detectors or a video camera to analyze the velocity and acceleration of each object.
Part II: Analysis
The objective of this section is to mathematically analyze the motion of an object rolling without slipping down an inclined plane. This section covers two approaches to this problem. The first part examines the forces acting on the object. This is followed by an examination using the conservation of energy.
The moment of inertia for each object is needed to calculate the acceleration on the ramp. First, derive an equation for acceleration in terms of the moment of inertia, then substitute the expression for the moment of inertia of each object.
The moment of inertia for geometrically symmetrical objects is often found in tables. See Appendix I of this document. Calculating the moment of inertia is a completely mathematical exercise. Appendix II includes the derivation of the moment of inertia for some basic geometric objects, including the disc and ring.
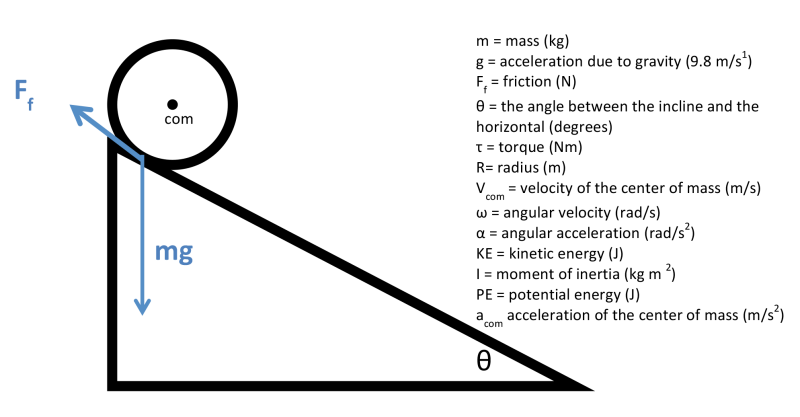
The goal is to find an expression for the acceleration of the center of mass of the object. After finding the equation for the translational acceleration, substitute that value into the kinematics equations to solve for time and velocity. Assume the object is rolling without slipping. For the purposes of this exercise, it will be assumed that the object rotates about the center of mass.

In the coordinate system shown, the object is in equilibrium in the Y direction.
The Normal
Force = m g cosθ
The object accelerates in the X direction. The sum of the forces in the X direction must equal the mass of the object times the acceleration of the center of mass.
ΣFx = macom
macom = mgsinθ -Ff
The object also rolls, so there must be a torque, τ, acting on the object. This torque is given by: τ = FfR (torque is represented by the Greek letter tau or τ).
The net torque on an object equals the moment of inertia of the object times the angular acceleration. (Angular acceleration is represented by the Greek letter alpha or α.) The net torque in this case is provided by the friction between the inclined plane and the object.
τNET = FfR= I α
Ff = I α / R
The angular acceleration can be expressed as:
α = acom/R
Substitute into the equation for the force of friction:
Ff = Iacom/R2
Substitute this expression for the force of friction into the equation for the sum of the forces in the X direction:
macom = mgsinθ -I α /R
macom = mgsinθ – Iacom /R2
Finally, solve for the acceleration of the center of mass of the object.
macom + (I/R2 )acom = mgsinθ
acom (1 + (I/mR2 )) = gsinθ
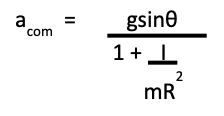
Substituting the moment of inertia for each object into this equation will give the translational acceleration for the object on an incline of angle θ.
Once the acceleration is found, the time can be calculated from the following kinematics equation:
d = ½ at2 + vit
Where:
d = the distance traveled (m)
a = the acceleration (m/s2 )
vi = the initial velocity (m/s)
t = the time (s)
The initial velocity is zero:
vi = 0 m/s
Therefore the time for the object to roll down the incline is:
t = √(2d/a)
Another way to approach this problem is to consider the energy of the system. The total energy of the system must be conserved at all times. Ignoring the energy lost to friction and sound, the energy in the system of an object rolling down an incline can be accounted for as mechanical energy in the following equation:
mgh = ½ mv2 + ½ Iω2mgh is the gravitational potential energy the object has at the top of the incline
½ mv2 is the translational kinetic energy the object has as it rolls down the incline
½ Iω2 is the rotational kinetic energy the object has as it rolls down the incline
m = mass (kg)
g = acceleration due to gravity (9.8 m/s2)
d = distance (m)
Ff = friction (N)
θ = the angle between the incline and the horizontal (degrees)
τ = torque (Nm)
R = radius (m)
vcom = velocity of the center of mass (m/s)
ω = angular velocity (rad/s)
α = angular acceleration (rad/s2)
KE = kinetic energy (J)
I = moment of inertia (kg m2)
PE = potential energy (J)
acom acceleration of the center of mass (m/s2)
At this point, substitute the expression for the moment of inertia for the given object, and solve for v. Once the final velocity is found, the kinematics equations can be used to find the time.
d = [(vf +vi)/2]t
Since vi is zero: t = 2d/vf
Notice the velocity of the object is independent of the mass and radius.Student Questions
- How does the moment of inertia affect the acceleration of a rolling object?
The moment of inertia is in the denominator of the acceleration equation. Therefore, the larger the moment of inertia, the smaller the acceleration. - How do the mass and the radius of the object affect the acceleration of a rolling object?
The acceleration is independent of the radius and the mass. - How does the acceleration of an object rolling down an incline compare with the
acceleration of an object sliding down an incline?
gsinθ is the acceleration for an object sliding without friction down an incline. The acceleration for a rolling object is always some fraction of this value. - How much time does it take for an object to roll down an incline?
This is a constant acceleration and can be applied to the kinematics equations:
The equation d = ½ at2 + vit gives the displacement of an object moving at a constant acceleration. In this activity, the object at the top of the incline starts at rest. Therefore:
vi = 0 m/s
d = ½ at2
vi = initial velocity (m/s)
d = distance (m)
a = acceleration (m/s2 )
Solving for t and substituting the acceleration for the rolling object gives the time required for an object to roll down an incline a distance S.
t = √(2d/a)
Ring: t = √(4d/gsinθ)
Disk: √(3d/gsinθ) - What is the minimum coefficient of friction required for a ring to roll down an incline
without slipping?
Ff = µFn = µmgcosθ
Ff R= τ = Iα
Ff is the force of friction (N)
τ is the net torque on the rolling object (Nm)
I is the moment of inertia (kgm2 )
acom is the acceleration of the center of mass of the object (m/s2 )
α is the angular acceleration (rad/s2 )
R is the radius of the object (m)
µmgcosθ = Iα/R
α = a/r
µmgcosθ = [(1/2 mR2 )/R](a/R)
µmgcosθ = [(1/2 mR2 )/R]( (2/3 gsinθ)/R)
µ = 1/3 TANθ - Design an experiment to measure the actual time it takes for the disc and the ring to roll
down an inclined plane at an angle of 5 to 10°. How does the measured value compare
with the predicted value? What are some sources of error? How can the experiment be
modified to give better results?
The experimental setup requires an inclined plane and some method of recording data. The simplest method is to use a timer. Data can also be collected using probeware sensors. Most probeware systems have a motion sensor that can be placed directly in front of or behind the moving objet. Data can be collected with a video camera. Sources of error may include human error and reaction time if students are using a manual timer. This can be considerable if the total time is only a few seconds. Inconsistencies in the surface of the ramp also contribute to error. If the objects do not roll straight, the path is longer than calculated. A longer distance eliminates some of the human error using the timer but increases the chance of the object turning during the roll. Making calculations over several tries and finding an average time is a good way to get better results. - How could the disc and ring be modified to affect their motion?
Changing the distribution of mass will change how the objects roll. If small masses were somehow added evenly to the objects in a way that did not inhibit their ability to roll, the objects would have a smaller acceleration.
Practice Problem
- Calculate the time for the disc to roll to the bottom of the incline by calculating the acceleration.
- Confirm the results using the conservation of energy
1) The moment of inertia for a solid disc is I = ½ mR2 .
a = ((gsinθ)/(1 + I/mR2 ))
a = 2/3 gsinθ
a = (2/3)(9.8 m/s2 )(sin 30°) = 3.26 m/s2
d = ½ a t2 +vit
vi = 0 m/s
t = √(2d/a) = √(2m/3.26m/s2 )
t = 0.78s
2) mgh = ½ mv 2 + ½ Iω 2
mgh = ½ mv 2 + ½(I)(v2 /R2 )
mgh = ½ mv 2 + ½(½ mR2 )(v2 /R2 )
gh = ½ v 2 + 1/4v2
gh = 3/4 v2
v = √(4/3 gh)
h =d(sin θ) = 1m (sin 30°) = 0.5m
v = 2.56 m/s
d = [(vf + vi)/2]t
vi = 0 m/s
t = 2d/vf
t = (2m)/(2.56 m/s)
t = 0.78 s
Appendix I
| Shape | Moment of Inertia | Final Translational Velocity | Translational Acceleration |
|---|---|---|---|
| Disc (cylinder) | 1⁄2 mR2 | √ (4⁄3 gh) | ⅔ gsinθ |
| Ring | mR2 | √(gh) | 1⁄2 gsinθ |
| Solid Sphere | 2⁄5 mR2 | √ (10⁄7 gh) | 5⁄7 gsinθ |
| Hollow Sphere | 2⁄3 mR2 | √ (6⁄5 gh) | 3⁄5 gsinθ |
Appendix II Derivation of the Moment of Inertia
A) Solid Cylinder:
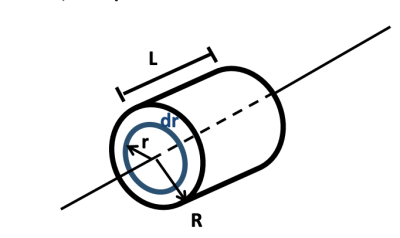
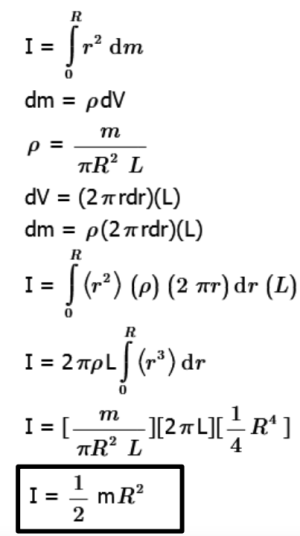
The equation for the moment of inertia is I = ∫r 2 dm, where dm is an infinitesimal portion of mass. The volume of a cylinder can be described in terms of length and radius. The mass can be described in terms of mass and volume. The density can be represented as ρ = m/V.
Note: In physics, density is often represented by the Greek symbol ρ, or rho. The lower case m is mass, and the capital V is volume. Be careful not to confuse this equation with p = mv, where p represents momentum and the lower case v represents velocity.
To find the moment of inertia for the solid cylinder or disc, consider the cylinder to be composed of concentric cylinders of radius r and length L along the axis of rotation. Calculate the mass of each cylinder and add them up by integrating. In order to get the mass in terms of radius, we will use the density. Density, ρ, is m/V. Mass can be represented as the density times the volume, ρV, and dm = ρdV. The volume, V, can be written in terms of r and L. The volume of a cylindrical shell with a very small thickness (dr) is the circumference of the shell (2πr) times the length (L) times the thickness (dr): dV =L2πrdr.
B) Cylindrical Shell (ring):
The moment of inertia of a ring is simple. All elements of mass dm are at a constant radius from the axis of rotation.
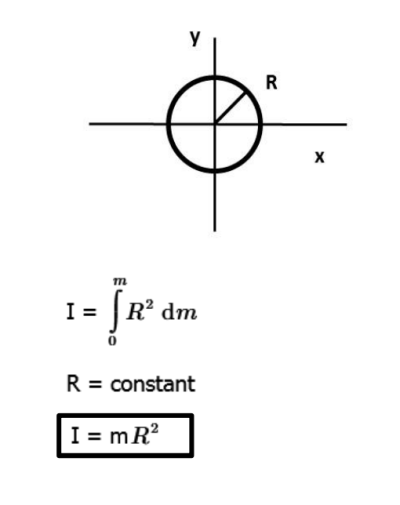
C) Solid Sphere:

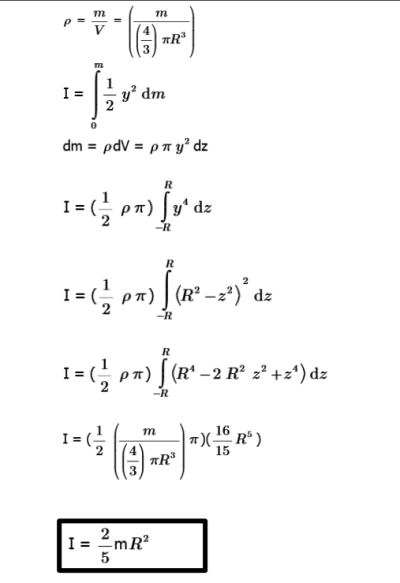
The moment of inertia is found by dividing the sphere into disks stacked on top of each other. Each disk has a moment of inertia I = ½ mR2 The mass of each disk can be represented by the density, ρ, times the volume. The volume is represented by the area, πy 2 , times the height dz (V = Adz = πy 2 dz). The dimension, y, can be represented in terms of z and R.
D) Spherical Shell:
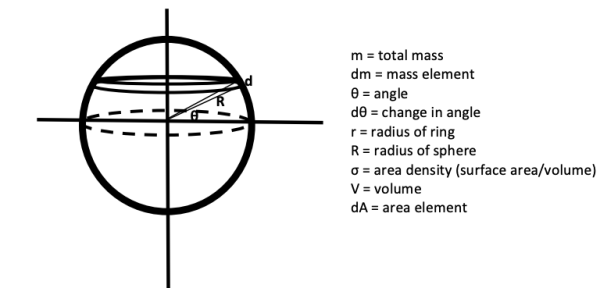
Integrate a stack of rings. The mass of each ring is dm. dm can be represented as the area density times the area.
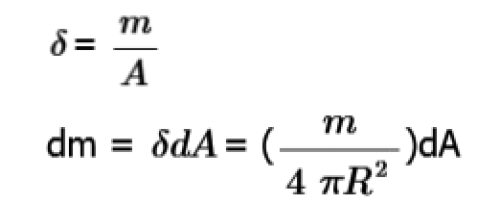
The element dA is the circumference of the ring times the thickness.
Circumference of the ring: 2πr
Radius of the ring r = Rcosθ
Circumference of the ring c = 2π Rcosθ
Thickness of the ring = R dθ

Related Products
*Next Generation Science Standards® is a registered trademark of Achieve. Neither Achieve nor the lead states and partners that developed the Next Generation Science Standards were involved in the production of, and do not endorse, these products.
About The Author
Carolina Staff
Carolina is teamed with teachers and continually provides valuable resources–articles, activities, and how-to videos–to help teachers in their classroom.









